აბაშის ხმა
Каталог статей
| მთავარი » სტატიები » Математика » Анализ |
Функция корреляции высота-высотаРазличие между функцией корреляции высота-высота и функцией автокорреляции очень мало. Как и в случае с функцией автокорреляции, мы суммируем произведение двух различных значений. Для функции автокорреляции эти значения представляют различные расстояния между точками. Для функции корреляции высота-высота мы вместо этого используем степень разности между точками. Для измерений АСМ мы обычно рассчитываем одномерную функцию корреляции высота-высота, основанную только на профилях вдоль быстрой оси сканирования. Следовательно, она может быть рассчитана из дискретных значений данных АСМ как 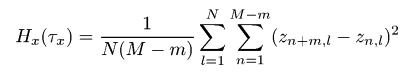 где m = τx/Δx. Таким образом, функция может быть рассчитана на дискретном наборе значений τx разделённом интервалом дискретизации Δx. Одномерная функция корреляции высота-высота нередко считается имеющей форму гауссовой, т.е. заданной следующим соотношением: 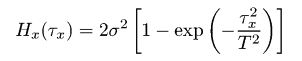 где σ обозначает среднеквадратичное отклонение высот и T обозначает длину автокорреляции. Для экспоненциальной функции корреляции высота-высота у нас получается следующее соотношение 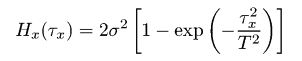 На следующем рисунке функция корреляции высота-высота построена для модели гауссовой поверхности. Она аппроксимирована формулой, приведённой выше. Результирующие значения σ и T полученные аппроксимацией функцией корреляции высота-высота практически те же, что и для функции автокорреляции. 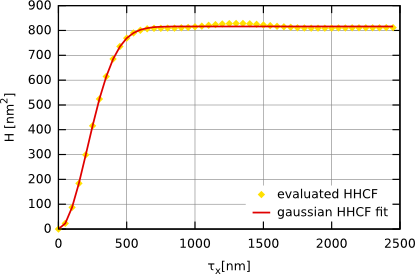 Функция корреляции высота-высота полученная для модели гауссовой случайно шероховатой поверхности с σ ≈ 20 nm и T ≈ 300 nm. | |
| ნანახია: 376 | |
| სულ კომენტარები: 0 | |
შესვლის ფორმა |
|---|
ძებნა |
|---|
მინი-ჩეთი |
|---|
საიტის მეგობრები |
|---|
სტატისტიკა |
|---|
