აბაშის ხმა
Каталог статей
| მთავარი » სტატიები » Математика » Анализ |
Функция спектральной плотности мощностиДвумерная функция спектральной плотности мощности может быть записана в терминах преобразования Фурье от функции автокорреляции
Подобно функции автокорреляции, мы также обычно рассчитываем одномерную функцию спектральной плотности мощности, которая задана уравнением 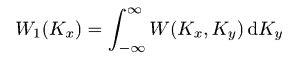 Эта функция может быть посчитана с помощью быстрого преобразования Фурье следующим образом: 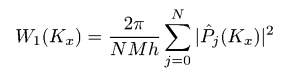 где Pj(Kx) - коэффициент Фурье для j-той строки, т.е. 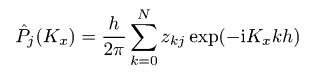 Если мы выберем гауссову функцию автокорреляции, соответствующее гауссово соотношение для функции спектральной плотности мощности будет следующим: 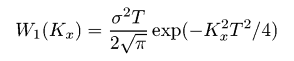 Для поверхности с экспоненциальной функцией автокорреляции мы имеем 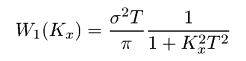 На следующем рисунке построены результирующая функция спектральной плотности мощности и её аппроксимация для той же самой поверхности, что использовалась для функции автокорреляции и функции корреляции высота-высота. Можно видеть, что функция может быть снова аппроксимирована гауссовой функцией спектральной плотности мощности. Результирующие значения σ и T практически те же самые, что и для аппроксимации функции автокорреляции и функции корреляции высота-высота. 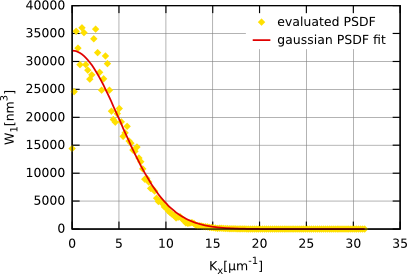 Функция спектральной плотности мощности полученная для данных, смоделированных с гауссовой функцией автокорреляции. Мы можем также ввести радиальную функцию спектральной плотности мощности Wr(K), которая, естественно, содержит ту же самую информацию, что и одномерная функция спектральной плотности мощности для изотропных шероховатых поверхностей: 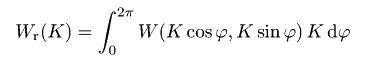 Для поверхности с гауссовой функцией автокорреляции эта функция может быть выражена как 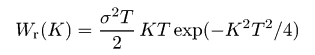 для поверхностей с экспоненциальной как 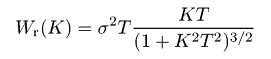 | |
| ნანახია: 415 | |
| სულ კომენტარები: 0 | |
შესვლის ფორმა |
|---|
ძებნა |
|---|
მინი-ჩეთი |
|---|
საიტის მეგობრები |
|---|
სტატისტიკა |
|---|