აბაშის ხმა
Каталог статей
| მთავარი » სტატიები » Математика » Численные методы оптимизации |
| Формирование М-задачи
Далеко не всегда имеет смысл разделять решение задачи линейного программирования на два этапа – вычисление начального опорного плана и определение оптимального плана. Вместо этого решается расширенная задача (М-задача). Она имеет другие опорные планы (один из них всегда легко указать), но те же решения (оптимальные планы), что и исходная задача. Рассмотрим наряду с исходной задачей (2.1) - (2.3) в канонической форме следующую расширенную задачу (М-задачу): Здесь М>0 – достаточно большое число. Начальный опорный план задачи (5.1) - (5.3) имеет вид
Переменные Таким образом, исходная задача линейного программирования с неизвестным заранее начальным опорным планом сводится к М-задаче, начальный опорный план которой известен. В процессе решения этой расширенной задачи можно либо вычислить оптимальный план задачи (2.1) - (2.3), либо убедиться в ее неразрешимости, если оказывается неразрешимой М-задача. В соответствии с вышеизложенным имеем: требуется решить задачу (2.12), (2.13), записанную в канонической форме. Введем искусственную неотрицательную переменную х9 и рассмотрим расширенную М-задачу
при условиях
(5.5)
где М – сколь угодно большая положительная величина. Как и в L-задаче, добавление только одной искусственной
переменной | |
| ნანახია: 305 | |
| სულ კომენტარები: 0 | |
შესვლის ფორმა |
|---|
ძებნა |
|---|
მინი-ჩეთი |
|---|
საიტის მეგობრები |
|---|
სტატისტიკა |
|---|
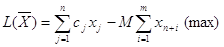 (5.1)
(5.1)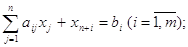 (5.2
(5.2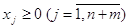
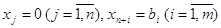
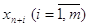 называются
искусственными переменными.
называются
искусственными переменными.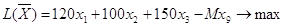 (5.4)
(5.4)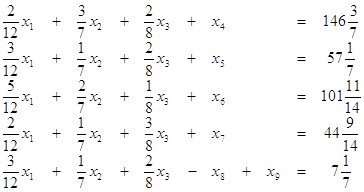
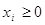 ,
где
,
где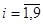 .
.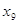 (вместо пяти) обусловлено тем,
что исходная задача уже содержит четыре единичных вектора условий А4, А5,
А6, А7.
(вместо пяти) обусловлено тем,
что исходная задача уже содержит четыре единичных вектора условий А4, А5,
А6, А7.