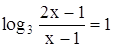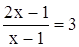აბაშის ხმა
Каталог статей
| მთავარი » სტატიები » Математика » Уравнения |
Логарифмические уравнения Логарифмическим уравнением называется уравнение, в котором неизвестное входит в виде аргумента логарифмической функции. Простейшим логарифмическим уравнением является уравнение вида где α - некоторое положительно число, отличное от единицы, b - любое действительное число. Логарифмическое уравнение (26) эквивалентно алгебраическому уравнению f(x) =αb. В простейшем случае, когда f(x) =x, логарифмическое уравнение (26) имеет решение x = αb. Множество решений логарифмического уравнения вида R(logax)=0 , где R - некоторый многочлен указанного неизвестного, находится следующим образом. Вводится новая переменная logax = y , и уравнение (25) решается как алгебраическое уравнение относительно y. После этого решаются простейшие логарифмические уравнения вида (25). П р и м е р 1. Решить уравнение
Относительно неизвестного log2x = y данное уравнение – квадратное: y²+y-2 = 0 Корни этого уравнения: y1=1,y2 =-2 , . Решая логарифмические уравнения log2x =1,log2x =-2, получаем решения логарифмического уравнения (27):x1= 2, x2=1/4 , . В некоторых случаях, для того чтобы свести решение логарифмического уравнения к последовательному решению алгебраического и простейших логарифмических уравнений,необходимо предварительно сделать
подходящие преобразования логарифмов, входящих в уравнение. Такими
преобразованиями могут быть преобразование суммы логарифмов двух величин в
логарифм произведения этих величин, переход от логарифма с одним основанием к
логарифму с другим основанием и т. д.
П р и м е р 2. Решить уравнение .
Для того чтобы свести решение данного уравнения к последовательному решению алгебраического и простейших логарифмических уравнений, необходимо прежде всего привести все логарифмы к одному основанию (здесь, например, к основанию 2). Для этого воспользуемся формулой, в силу которой равную
ему величину
Заменой .y² - y -6 = 0 Корни этого квадратного уравнения:y1= 3, y2 = -2 , . Решаем уравнения
П р и м е р 3. Решить уравнение
Преобразуя разность логарифмов двух величин в логарифм частного этих величин:
сводим данное уравнение к простейшему логарифмическому уравнению
| |
| ნანახია: 326 | |
| სულ კომენტარები: 0 | |
შესვლის ფორმა |
|---|
ძებნა |
|---|
მინი-ჩეთი |
|---|
საიტის მეგობრები |
|---|
სტატისტიკა |
|---|
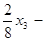 , (26)
, (26)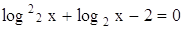 . (27)
. (27)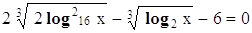 (28)
(28)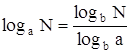
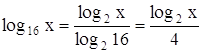 .
Подставив в уравнение (28) вместо
.
Подставив в уравнение (28) вместо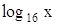
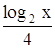 , получаем уравнение
, получаем уравнение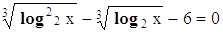
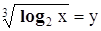 это
уравнение сводится к квадратному уравнению относительно неизвестного y:
это
уравнение сводится к квадратному уравнению относительно неизвестного y: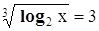 и
и 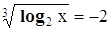 :
: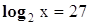
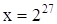 ,
,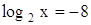
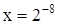 ,
,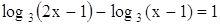
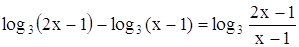 ,
,