აბაშის ხმა
Каталог статей
| მთავარი » სტატიები » Математика » Векторы |
Диагонали ромба взаимно перпендикулярны
| Рассмотрим доказательство некоторых теорем с помощью векторов.
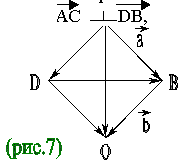
Теорема 1. Диагонали ромба взаимно перпендикулярны. Доказательство. ⇨⇨⇨⇨⇨⇨⇨⇨⇨⇨⇨⇨⇨⇨ Пусть АВСD – данный ромб (рис.7). Введем обозначения: АВ = а, ВС = в. Из определения ромба: АВ = DC = а, AD = ВС = в. ⇨⇨⇨ ⇨⇨ ⇨ По определению суммы и разности векторов АС = а + в; DВ = а – в. ⇨⇨ ⇨ Рассмотрим АС * DВ = (а + в )( а – в) = а2 – в2
Ч.т.д. | |||
| ნანახია: 772 | | |||
| სულ კომენტარები: 0 | |
მოგესალმები Гость
შესვლის ფორმა |
|---|
ძებნა |
|---|
მინი-ჩეთი |
|---|
საიტის მეგობრები |
|---|
სტატისტიკა |
|---|