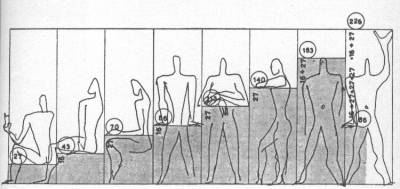
Модулор
В модулоре Ле Корбюзье каждое последующее членение связано с предыдущим
"золотым сечением". Понятие "золотого сечения" восходит из глубокой
древности. В геометрии Эвклида оно определено как деление отрезка в
крайнем и среднем отношениях, то есть деление отрезка, при котором
величина большей его части является средней пропорциональной всего
отрезка и его меньшей части. Введем обозначения: целое - С, большая
часть - а, меньшая - b. Правило "золотого сечения" выступит как
соотношение С/а=а/b. Это соотношение является иррациональным.
Распространенным и достаточно точным выражением его являются такие
величины: a = 0,618; b = 0,382. Приближенные целочисленные значения
"золотого сечения" можно получить при помощи чисел ряда Фибоначчи, в
котором каждое последующее число равно сумме двух предыдущих: 1, 2, 3,
5, 8, 13, 21... . Из этих числе составляется ряд целочисленных
отношений: 1: 2; 2 : 3; 3 : 5; 5 : 8; 8 : 13; 13 : 21;... В ряду,
начиная с отношения 5 : 8, все последующие выражает "золотое сечение".
Любое тело, предмет, вещь, геометрическая фигура, соотношение которых
соответствует "золотому сечению", отличаются строгой пропорциональностью
и производят наиболее приятное зрительное впечатление. В
садово-парковом искусстве применение правил пропорциональных соотношений
затруднено в связи с тем, что растительность, развиваясь,
увеличивается. Но, тем не менее, соотношения высоты растительной
группировки и площади экспозиции, а также растений внутри группировки,
растительности и архитектурных сооружений, ширин дорожек и цветников,
мельчайших деталей композиции должны строиться в соответствии с
правилами применяемых систем пропорций.
|

