Каталог статей

მთავარი » სტატიები » Наука » Золотое сечение
Золотой треугольник

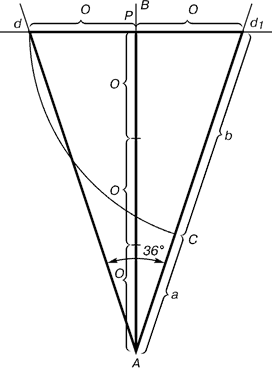Золотой треугольник

Замечательный пример "золотого сечения" представляет собой правильный пятиугольник - выпуклый и звездчаты  .

Из подобия треугольников ACD и ABE можем вывести уже известную пропорцию:

Таким образом, звездчатый пятиугольник также обладает "золотым сечением". Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.
Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.
Бытует легенда о том, что один из пифагорейцев больным попал в дом к незнакомым людям. Они старались его выходить, но болезнь не отступала. Не имея средств заплатить за лечение и уход, больной перед смертью попросил хозяина дома нарисовать у входа пятиконечную звезду, объяснив, что по этому знаку найдутся люди, которые вознаградят его. И на самом деле, через некоторое время один из путешествующих пифагорейцев заметил звезду и стал расспрашивать хозяина дома о том, каким образом она появились у входа. После рассказа хозяина гость щедро вознаградил его.
Пентаграмма была хорошо известна и в Древнем Египте. Но непосредственно как эмблема здоровья она была принята лишь в Древней Греции.
В настоящее время существует гипотеза, что пентаграмма - первичное понятие, а "золотое сечение" вторично. Пентаграмму никто не изобретал, ее только скопировали с натуры. Вид пятиконечной звезды имеют пяти-лепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов - пентаграмма - стала известна раньше, чем "золотая" пропорция.
Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.Построение правильного пятиугольника и пентаграммы



Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471...1528).
Пусть O - центр окружности, A - точка на окружности и Е - середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.Построение золотого
треугольника
Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения "золотого" прямоугольника.
კატეგორია: Золотое сечение | დაამატა: nukria (20.04.2012)
ნანახია: 487 | რეიტინგი: 0.0/0
სულ კომენტარები: 0
კომენტარის დამატება შეუძლიათ მხოლოდ დარეგისტრირებულ მომხმარებლებს
[ რეგისტრაცია | შესვლა ]
მოგესალმები Гость