აბაშის ხმა
Каталог статей
| მთავარი » სტატიები » Физика » Асимптота |
Геометрический смысл асимптоты
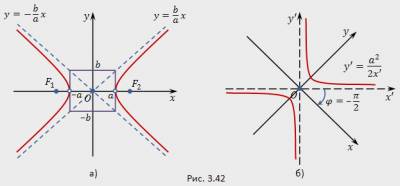 Геометрический смысл асимптоты Рассмотрим геометрический смысл асимптоты. Пусть М = (x, f (x)) – точка графика функции f, М 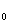 - -проекция этой точки на ось Ох, АВ – асимптота, q - угол между асимптотой и положительным направлением оси Ох, q ¹ 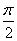 , ,MP – перпендикуляр, опущенный из точки М на асимптоту АВ, Q – точка пересечения прямой ММ 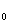 с сасимптотой АВ (рис.1). (рис.1) 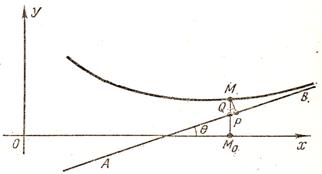 Тогда ММ 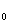 = f (x), QM = f (x), QM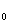 = kx + l, MQ = MM = kx + l, MQ = MM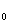 - QM - QM = f (x) – (kx +l), = f (x) – (kx +l),MP = MQ cos q. Таким образом, MP отличается от MQ лишь на не равный нулю множитель cos q, поэтому условия MQ ® 0 и MP ® 0 при х ® + ¥ (соответственно при х ® - ¥) эквивалентны, то есть lim MQ = 0, то и lim MP = 0, и наоборот. х ® + ¥ х ® + ¥ Отсюда следует, что асимптота может быть определена как прямая, расстояние до которой от графика функции, то есть отрезок МР, стремится к нулю, когда точка М = (x, f (x)) «стремится, оставаясь на графике, в бесконечность» (при х ® + ¥ или, соответственно, х ® - ¥). | |
| ნანახია: 656 | კომენტარი: 1 | |
| სულ კომენტარები: 0 | |
მოგესალმები Гость
სექციის კატეგორიები | |||||||
|---|---|---|---|---|---|---|---|
|
შესვლის ფორმა |
|---|
ძებნა |
|---|
მინი-ჩეთი |
|---|
საიტის მეგობრები |
|---|
სტატისტიკა |
|---|
სულ ონლაინში: 1 სტუმარი: 1 მომხმარებელი: 0 |
