Каталог статей

მთავარი » სტატიები » Физика » Асимптота
Нахождение асимптоты
 
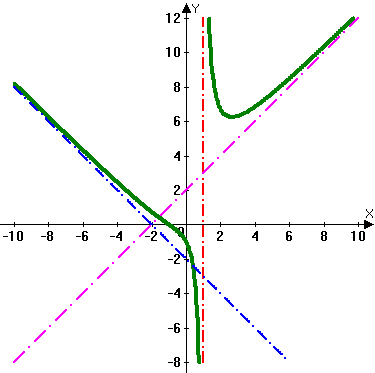Асимптота, так называемая прямая или кривая линия, которая, будучи
продолжена, приближается к другой кривой, но никогда не пересекает ее, так
что расстояние между ними делается бесконечно малой величиной.
Понятие асимптоты играет важную роль в математическом анализе. Они проводятся
при изучении свойств многих кривых (гиперболы, конхоиды, логарифмич. линии,
циссоиды и др.).
                                                                          
                     Нахождение асимптоты
                    
Пусть функция f (x) определена для всех x > а (соответственно для всех
x < а). Если существуют такие числа k и l, что f(x) - kx - l = 0 при х ® +
¥ (соответственно при х ® - ¥), то прямая
                                y = kx + l                                
называется асимптотой графика функции f (x) при x ® + ¥
(соответственно при х ® - ¥).
Существование асимптоты графика функции означает, что при х ® + ¥
(или х ® - ¥) функция ведёт себя «почти как линейная функция», то есть
отличается от линейной функции на бесконечно малую.
x - 3x - 2
Найдём, например, асимптоту графика функции y =       x +1
Разделив числитель на знаменатель по правилу деления многочленов,
2                         2
получим y = x - 4 +  x + 1   Так как   x + 1   = 0 при х ® ± ¥, то прямая y = x-4
является асимптотой графика данной функции как при х ® + ¥,
так и при х ® - ¥.
კატეგორია: Асимптота | დაამატა: nukria (25.04.2012)
ნანახია: 552 | კომენტარი: 1 | რეიტინგი: 0.0/0
სულ კომენტარები: 0
კომენტარის დამატება შეუძლიათ მხოლოდ დარეგისტრირებულ მომხმარებლებს
[ რეგისტრაცია | შესვლა ]
მოგესალმები Гость