Каталог статей

მთავარი » სტატიები » Физика » Фракталы
L-системы
 

L-системы.                              
Понятие L-систем, тесно связанное с самоподобными фракталами, появилось
только в 1968 году благодаря Аристриду Линденмайеру. Изначально L-системы были
введены при изучении формальных языков, а также использовались в биологических
моделях селекции. С их помощью можно строить многие известные самоподобные
фракталы, включая снежинку Коха и ковер Серпинского. Некоторые другие
классические построения, например кривые Пеано (работы Пеано, Гильберта,
Серпинского), также укладываются в эту схему. И конечно, L-системы открывают
путь к бесконечному разнообразию новых фракталов, что и послужило причиной их
широкого применения в компьютерной графике для построения фрактальных деревьев
и растений. Рассмотренные в данной курсовой работе L-системы ограничиваются
       случаем детерминированных L-систем и графикой на плоскости.       
Для графической реализации L-систем в качестве подсистемы вывода используется
так называемая тертл-графика (turtle – черепаха). При этом точка
(черепашка) движется по экрану дискретными шагами, как правило прочерчивая свой
след, но при необходимости может перемещаться без рисования. В нашем
распоряжении имеются три параметра (x,y,a), где (x,y) ---
координаты черепашки, a --- направление, в котором она смотрит.
Черепашка обучена интерпретировать и выполнять последовательность команд,
задаваемых кодовым словом, буквы которого читаются слева направо. Кодовое слово
представляет собой результат работы L-системы и может включать следующие буквы:
F --- переместиться вперед на один шаг, прорисовывая след.
b --- переместиться вперед на один шаг, НЕ прорисовывая след.
[  --- открыть ветвь (подробнее см. ниже)
]  --- закрыть ветвь (подробнее см. ниже)
+ --- увеличить угол a на величину q
- --- уменьшить угол a на величину q
Размер шага и величина приращения по углу q задаются заранее и остаются
неизменными для всех перемещений черепашки. Если начальное направление движения
а (угол, отсчитываемый от положительного направления оси Х) не указано, то
полагаем а равным нулю.
Несколько примеров иллюстрируют применение команд ветвления (обозначаются
],[) и вспомогательных переменных (обозначаются X, Y, и т.д.). Команды
ветвления используются для построения деревьев растений, а вспомогательные
переменные заметно облегчают построение некоторых L-систем.
Формально, детерминированная L-система состоит из алфавита, слова
инициализации, называемого аксиомой или инициатором, и набора
порождающих правил, указывающих, как следует преобразовывать слово при
переходе от уровня к уровню (от итерации к итерации). К примеру, можно заменять
букву F при помощи порождающего правила newf = F-F++F-F, что
соответствует L-системе для снежинки Коха, рассматриваемой ниже. Символы +, -,
], [ не обновляются, а просто остаются на тех местах, где они встретились.
Обновление букв в данном слове предполагается одновременным, то есть буквы
слова одного уровня обновляются раньше любой буквы следующего уровня.
L-система, соответствующая снежинке Коха (рис. 2.2.1), задается следующим
образом:
    p = p/3
Аксиома: F++F++F
Порождающее правило: newf = F-F++F-F
Графическое представление аксиомы F++F++F --- равносторонний треугольник.
Черепашка делает один шаг вперед, затем угол а увеличивается на 2p/3 и
черепашка делает еще один шаг.
На первом шаге каждая буква F в слове-инициаторе F++F++F заменяется на F-F++F-F:
                        (F-F++F-F)+(F-F++F-F)+(F-F++F-F)                        
Повторяя этот процесс, на втором шаге получим:
F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F+F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F+ F-
F++F-F- F-F++F-F++F-F++F-F-F-F++F-F
и т.д. Причем, убедившись на собственном опыте программирования L-систем
знаю, что для снежинки Коха на 20-й итерации порождающее правило занимает
несколько мегабайт текста !
       Вот еще некоторые фракталы, построенные с использованием L-системы:       
     Рис. 3.1. Дракон Хартера-Хатвея после 12-ти итераций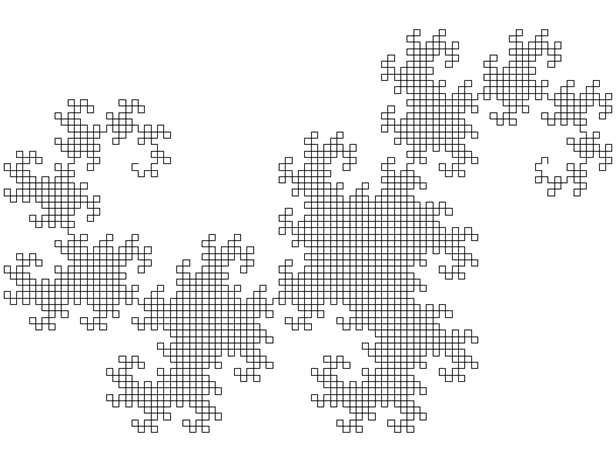
      
и его L-система:
     p = p/4
Аксиома: FX
Порождающее правило:         newf = F
     newx = X+YF+
     newy = -FX-Y
     Рис 3.2. Дерево после 5-ти итераций
      
и его L-система:
     p = p/7
Аксиома: F
Порождающее правило:         newf = F[+F]F[-F]F
     Рис. 3.3. Квадрат Госпера после 2-х итераций [2]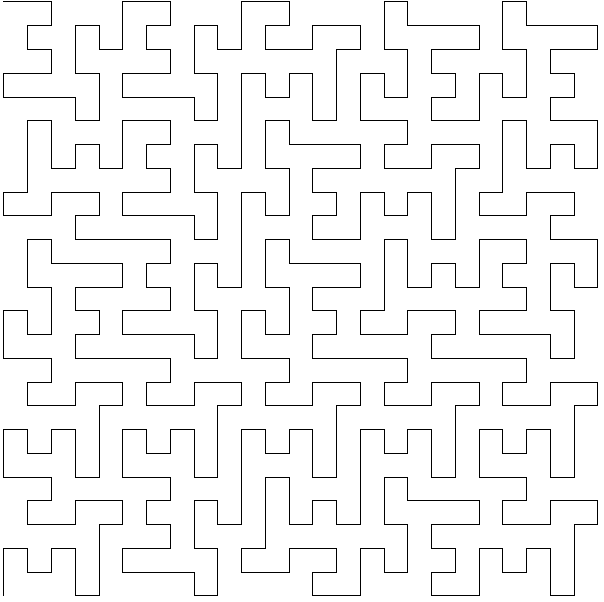
      
и его L-система:
     p = p/2
Аксиома: -FX
Порождающее правило:         newf = F
newx=+FYFY-FX-FX+FY+FYFX+FY-FXFX-FY-FX+FYFXFX-FY-FXFY+FY+FX-FX-FY+FY+FXFX
     newy=FYFY-FX-FX+FY+FY-FX-FXFY+FX+FYFYFX-FY+FX+FYFY+FX-FYFX-FX-FY+FY+FXFX-
კატეგორია: Фракталы | დაამატა: nukria (25.04.2012)
ნანახია: 571 | კომენტარი: 1 | რეიტინგი: 0.0/0
სულ კომენტარები: 0
კომენტარის დამატება შეუძლიათ მხოლოდ დარეგისტრირებულ მომხმარებლებს
[ რეგისტრაცია | შესვლა ]
მოგესალმები Гость