Каталог статей

მთავარი » სტატიები » Физика » Фракталы
Снежинка Коха

     
Снежинка Коха
.                           
Граница снежинки, придуманной Гельгом фон Кохом в 1904 году (рис.2.2.1),
описывается кривой, составленной их трех одинаковых фракталов размерности d ~
1,2618. Каждая треть снежинки строится итеративно, начиная с одной из сторон
равностороннего треугольника. Пусть Ko --- начальный отрезок. Уберем
среднюю треть и добавим два новых отрезка такой же длины, как показано на рис.
2.2.2. Назовем полученное множество K1 . Повторим данную процедуру
многократно, на каждом шаге заменяя среднюю треть двумя новыми отрезками.
Обозначим через Kn фигуру, полученную после n-го шага.
Интуитивно ясно, что последовательность кривых Kn при n стремящемся к
бесконечности сходится к некоторой предельной кривой К. Рассмотрим некоторые
свойства этой кривой.
Если взять копию К, уменьшенную в три раза (r = 1/3), То всё множество К
можно составить из N = 4 таких копий. Следовательно, отношение самоподобия
(2.1) выполняется при указанных N и r, а размерность фрактала будет:
                           d = log(4)/log(3) ~ 1,2618                           
     Рис 2.2.1. Снежинка Коха.
                                                                              
      Еще одно важное свойство, которым обладает граница снежинки Коха --- ее
бесконечная длина. Это может показаться удивительным, потому что мы привыкли
иметь дело с кривыми из курса математического анализа. Обычно гладкие или
хотя бы кусочно-гладкие кривые всегда имеют конечную длину (в чем можно
убедиться интегрированием). Мандельброт в этой связи опубликовал ряд
увлекательных работ, в которых исследуется вопрос об измерении длины
береговой линии Великобритании. В качестве модели он
     Рис. 2.2.2. Построение снежинки Коха.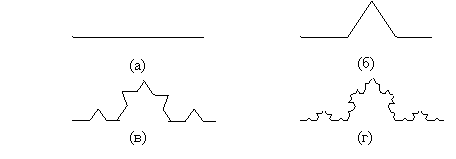
      
использовал фрактальную кривую, напоминающую границу снежинки за тем
исключением, что в нее введен элемент случайности, учитывающий случайность в
природе. В результате оказалось, что кривая, описывающая береговую линию,
имеет бесконечную длину.
Доказательство приводится в [1].

კატეგორია: Фракталы | დაამატა: nukria (25.04.2012)
ნანახია: 1114 | კომენტარი: 1 | რეიტინგი: 0.0/0
სულ კომენტარები: 0
კომენტარის დამატება შეუძლიათ მხოლოდ დარეგისტრირებულ მომხმარებლებს
[ რეგისტრაცია | შესვლა ]
მოგესალმები Гость