Каталог статей

მთავარი » სტატიები » Физика » Метод Зойтендейка
Линейный поиск

Линейный поиск

Только что было показано, как строить возможное направление спуска или убедиться, 

что текущая точка удовлетворяет условиям Куна—Таккера. 

Пусть
теперь хk —текущая точка, а dk-возможное направление спуска. 

В качестве следующей точки xk+1 берется  , где длина шага К& определяется из 

реше­ния следующей задачи одномерной минимизации:

Минимизировать при условиях  

Предположим
теперь, что АT=(А1T, А2T), а bT=(b1T, b2T), так что   и   . 

Тогда задачу одномерной мини­мизации
можно упростить следующим образом. Во-первых, за­метим,
что 

Ехk=е и Еdk=0, так что
ограничение  излишне. Так как   и    для всех l³0. Таким образом,
рассматриваемая 

задача приводится к следующей задаче линейного поиска;


 Алгоритм метода Зойтендейка (случай линейных ограничений)

Ниже приведен алгоритм метода Зойтендейка для минимизации дифференцируемой функции f

при условии,что                                        

Начальный этап.
Найти начальную допустимую точку х1, для которой  . Положить k
= 1 и перейти к основ­ному этапу.


Основной этап.
Шаг 1. Пусть задан хk. Предположим, что
АT=(А1T, А2T), а bT=(b1T, b2T), так что  . Взять в
качестве dk оптимальное
решение следующей задачи (заметим, что вместо этой задачи можно
использовать Р2 или РЗ):
 

Если  , то остановиться;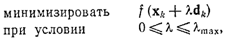
хk—точка Куна—Таккера, В противном случае перейти к
шагу 2.

 

Шаг 2. Положить   равным оптимальному решению еле-., дующей задачи
линейного поиска: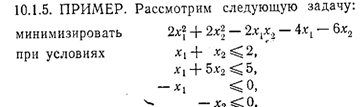 


где  определяется в соответствии с (1). Положить  , определить новое множество активных 
ограниче­ний в и переопределить А1 и А2. Заменить k на k+1 и перейти к
шагу 1.

Заметим, чт. Решим задачу методом Зойтендейка, взяв в качестве начальной точки  . Каждая итерация алгоритма содержит решение подзадачи,
определенной в описании шага 1, для нахождения направления, а затем линейный поиск вдоль этого направления.

Итерация 1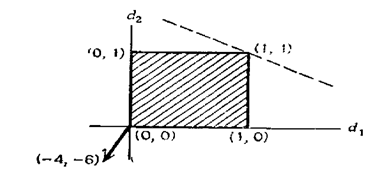
Поиск
направления. В точке   имеем . Кроме того, в точке x1
активными являются толь­ко ограничения неотрицательности переменных, так что l = {3,4}. Задача для нахождения направления
имеет вид

Рис. 2

Эту задачу можно
решить симплекс методом для решения задач линейного программирования. На
рисунке 2 показана допустимая область этой задачи.

Линейный поиск.
Теперь, двигаясь из точки (0, 0) вдоль направления (1, 1), нужно найти точку, в которой значение це­левой функции   минимально. Любая точка может быть записана в виде  ,
а целевая функция в этой точке принимает вид   . Максимальное значение коэффициента l, для 

ко­торого точка  допустима, вычисляется по формулам  и равно

Следовательно,
если    —новая точка, то значение
   по­лучается из решения следующей задачи
одномерной миними­зации:

минимизировать    —10+2

при условии         0£     £    .

Очевидно, что
решением является    ,
так что

Итерация 2

Поиск, направления. В точке  имеем               с 3.

Кроме того,
множество активных ограничений
в точке х2 равно l={2}, так что направление
движения получается из решения следующей задачи:

минимизировать при условии

Читатель может
проверить на рис. 3, что оптимальным реше­нием
этой задачи линейного программирования является точка   , а
соответствующее значение целевой функции равно               .

Линейный поиск.
При начальной точке х2 любая точка в на­правлении d2 может быть
представлена в виде    Соответствующее
ей значение целевой функ­ции равно

Максимальное значение l для которого точка Х2+ld2 остается допустимой, определяется в соответствия с (1) следующим образом:

Таким образом, в
качестве ^ берется оптимальное решение сле­дующей задачи:

минимизировать при условии        

Оптимальным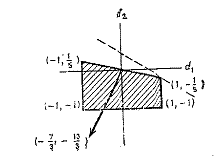
решением этой задачи является  , так что 



Рис 4.

Итерация 3

Поиск направления. В точке х3=имее  Кроме того, множество активных ограни­чений
в точке хз равно l = {2},
так что направление движения получается из решения следующей задачи:

Можно легко
проверить по рис. 4. что     действительно является решением этой задачи ли­нейного
программирования. Соответствующее значение целевой функции равно нулю, и
процедура заканчивается. Более того, точка     является точкой
Куна—Таккера.

В этой конкретной
задаче функция f выпукла, и по теореме
4.3.7 точка х является оптимальным решением.

Таблица 1



Результаты
вычислений по методу Зойтендейка
для случая линейных ограничений 

Рис. 5. Поиск решения
методом Зойтендейка (случай линейных ограничений).

В табл. 1 приведены результаты вычислений для рассмо­тренной
задачи. На рис. 10.5 изображен процесс
поиска решения в соответствии с описанным алгоритмом.

კატეგორია: Метод Зойтендейка | დაამატა: nukria (26.04.2012)
ნანახია: 524 | კომენტარი: 1 | რეიტინგი: 0.0/0
სულ კომენტარები: 0
კომენტარის დამატება შეუძლიათ მხოლოდ დარეგისტრირებულ მომხმარებლებს
[ რეგისტრაცია | შესვლა ]
მოგესალმები Гость