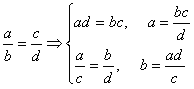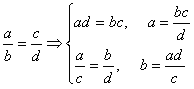Каталог статей
Алгебраические формулы
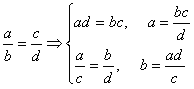 =±Ö1-sin2a=(1-tg2a/2)/(1+tg2a/2)
|
sina=±Ö1/1+ctg2a=(2tga/2)/(1+tg2a/2)
|
|
cos(a b)=sinasinb b)=sinasinb cosacosb cosacosb
|
sin(a±b)=sinacosb±sinbcosa
|
|
tg(a+b)=sin(a+b)/cos(a+b)=(tga+tgb)/(1-tgatgb)
|
tg(a-b)=(tga-tgb)/(1+tgatgb)
|
|
ctg(a+b)=(ctgactgb-1)/(ctga+ctgb)
|
ctg(a-b)=(ctgactgb+1)/(ctgb-ctga)
|
|
sin2a=2sinacosa=(2tga)/(1+tg2a)
|
cos2a=cos2a-sin2a=(1-tg2a)/(1+tg2a)=2cos2a-1=1-2sin2a
|
|
tg2a=2tga/(1-tg2a) ctg2a=(ctg2a-1)/2ctga
|
ctg2a=(ctg2a-1)/2ctga
|
|
cos2a/2=1+cosa/2 cos2a=(1+cos2a)/2
|
sin2a/2=1-cosa/2 sin2a=(1-cos2a)/2
|
|
cosa/2=±Ö1+cosa/2
|
sina/2=±Ö1-cosa/2
|
|
tga/2=±Ö1-cosa/1+cosa=(sina)/(1+cosa)=(1-cosa)/sina
|
ctga/2=±Ö1+cosa/1-cosa=sina/(1-cosa)=(1+cosa)/sina
|
|
sina+cosa=Ö2
cos(P/4-a)
|
sina-cosa=Ö2
sin(a-P/4)
|
|
cosa-sina=Ö2
sin(P/4-a)
|
cosa+cosb=2cos(a+b)/2cos(a-b)/2
|
|
cosa-cosb=-2sin(a+b)/2sin(a-b)/2
|
sina+sinb=2sin(a+b)/2cos(a-b)/2
|
|
sina-sinb=2sin(a-b)/2cos(a+b)/2
|
tga±tgb=(sin(a±b))/cosacosb
|
|
cosacosb=1/2(cos(a-b)+cos(a+b))
|
sinasinb=1/2(cos(a-b)-cos(a+b))
|
|
sinacosb=1/2(sin(a+b)+sin(a-b))
|
tga=(2tga/2)/(1-tg2a/2)
|
|
cosa=±Ö1-sin2a=(1-tg2a/2)/(1+tg2a/2)
|
sina=±Ö1/1+ctg2a=(2tga/2)/(1+tg2a/2)
|
|
cos(a b)=sinasinb b)=sinasinb cosacosb cosacosb
|
sin(a±b)=sinacosb±sinbcosa
|
|
tg(a+b)=sin(a+b)/cos(a+b)=(tga+tgb)/(1-tgatgb)
|
tg(a-b)=(tga-tgb)/(1+tgatgb)
|
|
ctg(a+b)=(ctgactgb-1)/(ctga+ctgb)
|
ctg(a-b)=(ctgactgb+1)/(ctgb-ctga)
|
|
sin2a=2sinacosa=(2tga)/(1+tg2a)
|
cos2a=cos2a-sin2a=(1-tg2a)/(1+tg2a)=2cos2a-1=1-2sin2a
|
|
tg2a=2tga/(1-tg2a) ctg2a=(ctg2a-1)/2ctga
|
ctg2a=(ctg2a-1)/2ctga
|
|
cos2a/2=1+cosa/2 cos2a=(1+cos2a)/2
|
sin2a/2=1-cosa/2 sin2a=(1-cos2a)/2
|
|
cosa/2=±Ö1+cosa/2
|
sina/2=±Ö1-cosa/2
|
|
tga/2=±Ö1-cosa/1+cosa=(sina)/(1+cosa)=(1-cosa)/sina
|
ctga/2=±Ö1+cosa/1-cosa=sina/(1-cosa)=(1+cosa)/sina
|
|
sina+cosa=Ö2
cos(P/4-a)
|
sina-cosa=Ö2
sin(a-P/4)
|
|
cosa-sina=Ö2
sin(P/4-a)
|
cosa+cosb=2cos(a+b)/2cos(a-b)/2
|
|
cosa-cosb=-2sin(a+b)/2sin(a-b)/2
|
sina+sinb=2sin(a+b)/2cos(a-b)/2
|
|
sina-sinb=2sin(a-b)/2cos(a+b)/2
|
tga±tgb=(sin(a±b))/cosacosb
|
|
cosacosb=1/2(cos(a-b)+cos(a+b))
|
sinasinb=1/2(cos(a-b)-cos(a+b))
|
|
sinacosb=1/2(sin(a+b)+sin(a-b))
|
tga=(2tga/2)/(1-tg2a/2) |
|
| კატეგორია: Алгебра | დაამატა: nukria (25.04.2012)
|
| ნანახია: 1130 |
| რეიტინგი: 0.0/0 |
კომენტარის დამატება შეუძლიათ მხოლოდ დარეგისტრირებულ მომხმარებლებს
[
რეგისტრაცია |
შესვლა ]