აბაშის ხმა
Каталог статей
| მთავარი » სტატიები » Математика » Анализ |
Функция автокорреляцииФункция автокорреляции задаётся как 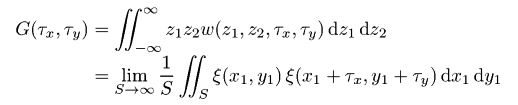 где z1 и z2 - значения высоты в точках (x1, y1), (x2, y2); при этом τx = x1 − x2 и τy = y1 − y2. Функция w(z1, z2, τx, τy) обозначает двумерную плотность вероятности случайной функции ξ(x, y), соответствующей точкам (x1, y1), (x2, y2) и расстоянию между этими точками τ. Из дискретных данных АСМ можно извлечь эту функцию в виде 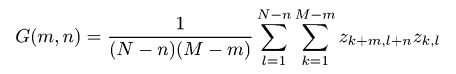 где m = τx/Δx, n = τy/Δy. Следовательно, эта функия может быть рассчитана для дискретного набора значений τx и τy, разделённых интервалами дискретизации Δx и Δy, соответственно. Двумерная функция автокореляции может быть посчитана с помощью меню → → . Для измерений АСМ мы обычно рассчитываем одномерную функцию автокорреляции основанную на профилях вдоль оси быстрого сканирования. Она может, следовательно, рассчитываться из дискретных данных АСМ как 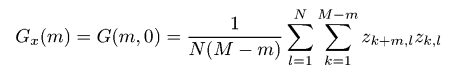 Одномерная функция автокорреляции нередко считается имеющей форму гауссовой, т.е. заданной следующим соотношением: 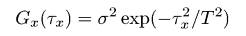 где σ обозначает среднеквадратичное отклонение высот и T обозначает длину автокорреляции. Для экспоненциальной функции автокорреляции у нас получается следующее соотношение 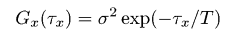 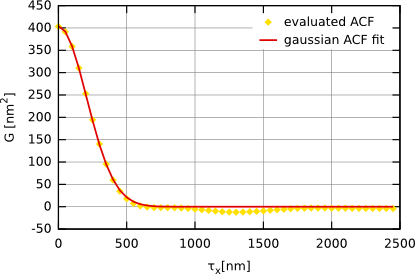 Функция автокорреляции, полученная для модели гауссово случайной шероховатой поверхности (т.е. с гауссовой функцией автокорреляции) с σ ≈ 20 nm и T ≈ 300 nm. Мы можем также ввести радиально усреднённую функцию автокорреляции Gr(τ), которая, естественно, содержит ту же самую информацию, что и одномерная функция автокорреляции для изотропных шероховатых поверхностей: 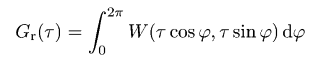 ПримечаниеДля оптических измерений (т.е. спектроскопической рефлектометрии, эллипсометрии) гауссова функция автокорреляции обычно ожидается достаточно хорошо совпадающей со свойствами поверхности. Однако, некоторые статьи связанные с ростом поверхности и оксидированием обычно предполагают, что экспоненциальная форма ближе к реальности. | |
| ნანახია: 427 | კომენტარი: 1 | |
| სულ კომენტარები: 0 | |
შესვლის ფორმა |
|---|
ძებნა |
|---|
მინი-ჩეთი |
|---|
საიტის მეგობრები |
|---|
სტატისტიკა |
|---|
