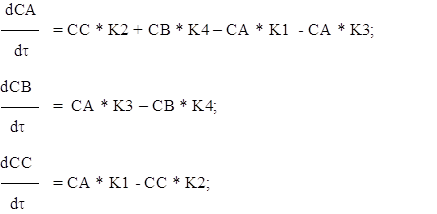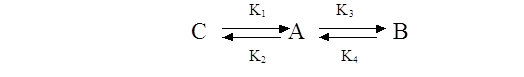| Постановка задачи
Многие
процессы химической технологии описываются СДУ - начиная от кинетических
исследований и заканчивая химическими технологическими процессами. В
основу математических способов описания процессов положены СДУ и
СЛАУ. Эти уравнения описывают материальные и тепловые
балансы объектов химической технологии, а так же структуры
потоков технических веществ в этих аппаратах.
Для получения, распределения технологических параметров во времени и в пространстве
(в пределах объекта), необходимо произвести СДУ методом, которых дал бы высокую точность решения при минималььных затратах
времени на решение, потому что ЭВМ должна работать в режиме реального
времени и успевать за ходом технологического процесса. Если время на решение задачи большое, то
управляющее воздействие, выработанное на ЭВМ может привести к отрицательным
воздействиям. Методов решения существует очень много. В данной работе будет рассмотрен метод решения СДУ методом Рунге-Кутта
4 порядка.
Для удобства
работы на ЭВМ, необходимо данную кинетическую схему преобразовать в удобный для
работы на компьютере вид. Для этого необходимо кинетическую схему процесса
представить в виде уравнений. При рассмотрении кинетической схемы процесса
необходимо учитывать коэффициенты скоростей реакций. Но, так как процесс
протекает при изотермических условиях, коэффициенты скоростей реакций можно
считать за константы скоростей химической реакции. Из приведенной ниже схемы мы
можем составить ряд дифференциальных уравнений, учитывающих изотермичность
процесса.
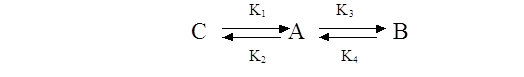
Так как
коэффициенты K1,K2,K3,K4 являются константами, то можно уравнение записать в
следущем виде.
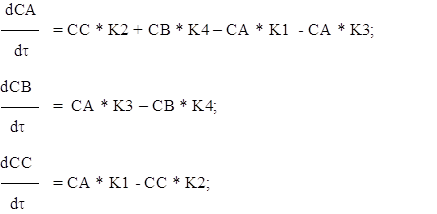
Для преобразования данных дифференциальных
уравнений для использования их в расчетах тепловых и кинетических схем методами
Рунге-Кутты необходимо подставлять вместо производных значений концентраций,
значения концентраций данных в начале процесса. Это обусловлено тем, что метод
Рунге-Кутты четвертого порядка, который будет использован для расчета
кинетической схемы процесса. Так как этот метод требует сведений только об
одной точке и значений функции.
|