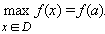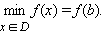Монотонность функцийПеречислим свойства монотонных функций (предполагается, что все функции определены на некотором промежутке D ). - Сумма нескольких возрастающих функций является возрастающей функцией.
- Произведение неотрицательных возрастающих функций есть возрастающая функция.
- Если функцияf возрастает, то функции cf ( c > 0) и f + c также возрастают, а функция cf ( c < 0) убывает. Здесь c – некоторая константа.
- Если функция f возрастает и сохраняет знак, то функция 1/ f убывает.
- Если функция f f возрастает и неотрицательна, то ƒⁿ где n Є N , также возрастает.
- Если функция f возрастает и n – нечетное число, то ƒⁿ также возрастает.
- Композиция g ( f ( x )) возрастающих функций f и g также возрастает.
Аналогичные утверждения можно сформулировать и для убывающей функции. 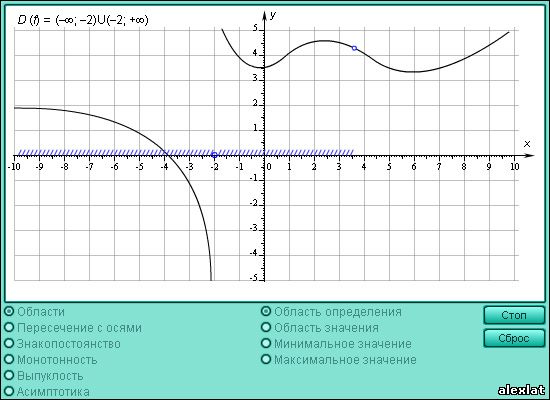
Модель 1.9. Свойства функции. Точка a называется точкой максимума функции f , если существует такая ε-окрестность точки a , что для любого x из этой окрестности выполняется неравенство f ( a ) ≥ f ( x ). Точка a называется точкой минимума функцииf , если существует такая ε-окрестность точки a , что для любого x из этой окрестности выполняется неравенство f ( a ) ≤ f ( x ). Точки, в которых достигается максимум или минимум функции, называются точками экстремума . В точке экстремума происходит смена характера монотонности функции. Так, слева от точки экстремума функция может возрастать, а справа – убывать. Согласно определению, точка экстремума должна быть внутренней точкой области определения. Если для любого x ЄD (x≠ a) выполняется неравенство f ( x ) ≤ f ( a ) ( αЄD) то точка a называется точкой наибольшего значения функции на множестве D : 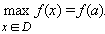 Если для любого x ЄD ( x ≠ b ) выполняется неравенство f ( x ) > f ( b )( bЄD) то точка b называется точкой наименьшего значения функции на множестве D . 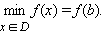
Синус, косинус, тангенс и котангенс часто называют основными тригонометрическими функциями. Иногда рассматривают еде две основные тригонометрические функции - секанс и косеканс (обозначаются sec и cosec соответственно). Для того, чтобы понять, почему основных тригонометрический функций именно шесть, заметим, что тригонометрические функции острого угла можно определить как отношения сторон прямоугольного треугольника с острым углом
|