აბაშის ხმა
Каталог статей
| მთავარი » სტატიები » Математика » Векторы |
| Рассмотрим теперь решение задач с помощью векторов.
Задача 1. Даны два вектора AB и CD, причем А( -1; 2; 4), В ( -4; 5; 4), С( -1; -2; 2) и D(2; 1;5). Определить, перпендикулярны они друг другу или нет. Решение. Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD = (3; 3; 3). Вычислим теперь скалярное произведение этих векторов: АВ х СD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0. Последнее и означает, что АВ _ СD.
Задача 2. Дан произвольный треугольник АВС. Доказать, что можно построить треугольник, стороны которого равны и параллельны медианам треугольника АВС.
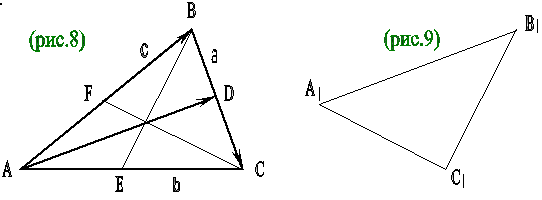
Решение. Обозначим медианы треугольника АВС через ВЕ, СF и обозначим векторы, идущие вдоль сторон треугольника АВС, через а, в, с: ВС = а, СА = в, АВ = с (рис.8). Тогда АD =
АВ + ВD = АВ + аналогично определяются и другие медианы: ВЕ = а + Так как, в силу условия замкнутости ВС + СА + АВ = а + в + с =0, то мы имеем: АD + ВЕ + СF = ( с + Следовательно, отложив от точки В, вектор В1С1 = ВЕ и от точки С1 – вектор С1D1 = СF, мы получим. А1В1 + В1С1 + С1D1 = АD + ВЕ + СF = 0. А это значит (в силу условия замкнутости), что ломаная А1В1С1D1 является замкнутой, т.е. точка D1 совпадает с А1. Таким образом, мы получаем треугольник А1В1С1 (рис.9), стороны которого равны и параллельны медианам АD, ВЕ, СF исходного треугольника. | |
| ნანახია: 668 | |
| სულ კომენტარები: 0 | |
შესვლის ფორმა |
|---|
ძებნა |
|---|
მინი-ჩეთი |
|---|
საიტის მეგობრები |
|---|
სტატისტიკა |
|---|
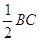 =
с +
=
с +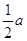
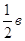
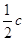
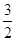 ( а + в + с) =
( а + в + с) = 