აბაშის ხმა
Каталог статей
| მთავარი » სტატიები » Математика » Векторы |
| Задача 3.
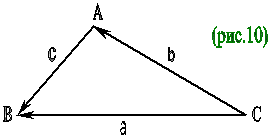
Доказать, что для любого треугольника имеет место формула с2 = а2 + в2 – 2ав х соs С (теорема косинусов)
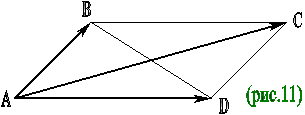
Решение. Положим: а = СВ, в = СА, с = АВ (рис.10). Тогда с = а – в, и мы имеем (учитывая, что угол между векторами а и в равен С): с2 = ( а – в )2 = а2 – 2ав + в2 = а2 – 2ав х соs С + в2. Задача 4. Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Решение. Пусть четырехугольник АВСD – параллелограмм (рис.11). Имеем векторные равенства АВ + AD = АС, АВ – АD = DВ. Возведем эти равенства в квадрат. Получим: АВ2 + 2 АВ х АD + АD2 = АС2, АВ2 – 2АВ х АD + АD2 = DВ2 Сложим эти равенства почленно. Получим: 2АВ2 + 2 АD2 = АС2 + DВ2. Так как у параллелограмма противолежащие стороны равны, то это равенство и означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, что и требовалось доказать.
Задача 5. Даны три точки: А ( 1; 1), В ( -1; 0), С ( 0; 1). найдите такую точку D ( х; y), чтобы векторы АВ и СD были равны. Решение. Вектор АВ имеет координаты –2, -1. Вектор СD имеет координаты х – 0, y –1. Так как АВ = СD, то х – 0 = -2, y –1 = -1. Отсюда находим координаты точки D: х = -2, y = 0.
Задача 6. Даны два вектора АВ и СD, причем А ( -1; 2; 4), В ( -4; 5; 4), С ( -1; -2; 2), D ( 2; 1; 5).Определить, перпендикулярны они друг другу или нет. Решение. Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD ( 3; 3; 3). Вычислим теперь скалярное произведение этих векторов: AB х CD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.
| |
| ნანახია: 443 | |
| სულ კომენტარები: 0 | |
შესვლის ფორმა |
|---|
ძებნა |
|---|
მინი-ჩეთი |
|---|
საიტის მეგობრები |
|---|
სტატისტიკა |
|---|